Researchers
Carlos E. S. Cesnik – Clarence L. (Kelly) Johnson Professor of Aerospace Engineering, University of Michigan
Michael Jones – Graduate Student Research Assistant, University of Michigan
Ana C. Meinicke – Graduate Student Research Assistant, University of Michigan
Solving the inverse problem with Scientific Machine Learning requires data to train its algorithms. Our goal is to determine the best way to obtain the required training data for the entire flight envelope in a timely manner and with the appropriate level of fidelity.
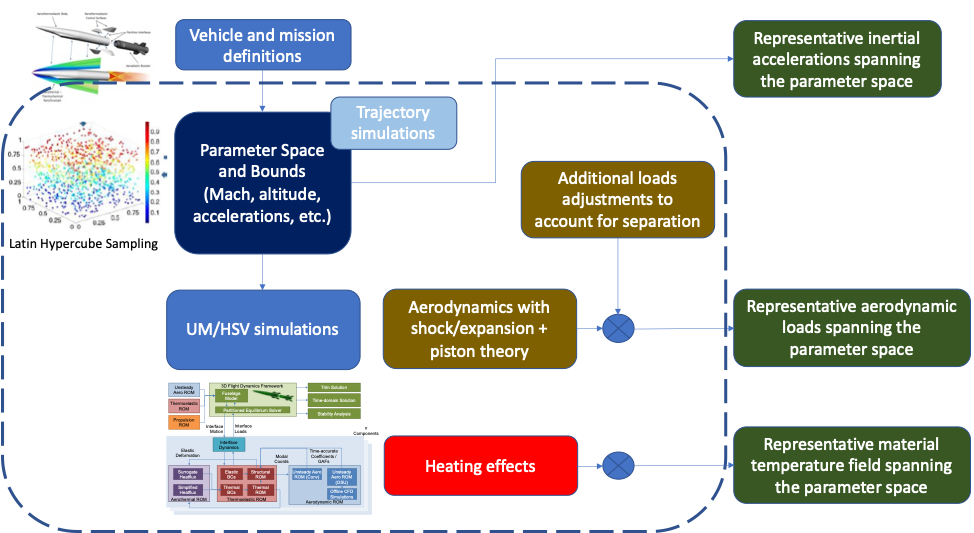
The training data for this problem will relate the temperature and structural deformation to the aerodynamic loading distribution, the inertial loading, and aeroheating. The aerothermoelastic solution used to calculate the temperature, deformation, and loading distributions will be developed here and will take advantage of the University of Michigan’s High-Speed Vehicle (UM/HSV) framework, a multi-physics, multi-fidelity simulation framework, and the finite element solver Abaqus. The UM/HSV (Klock & Cesnik, 2014) integrates aero-thermo-elastic-propulsive models to simulate a high-speed vehicle through its trajectory. With it, one can conduct stability analysis, flight trimming, dynamic simulation, and closed-loop control evaluation. It takes advantage of engineering and reduced-order models to capture the various effects impacting the flight of the vehicle as seen illustrated in Figure 1.
The aerothermoelastic modeling is conducted under the assumption that the highest fidelity model possible is not required to generate the appropriate excitation loads for the detailed thermal and elastic training data. Simplified loading distribution estimations are acceptable if they are representative of the solutions and spans the loading distribution space of interest. One of the major goals of our research is to determine the importance of loading model accuracy to the FAST methodology. The loading distribution space will be defined based on numerical and experimental test cases. The numerical model is the IC3X vehicle developed by the AFRL Munitions Directorate (Witeof, Z. D., and Neergaard, 2014) and modified by the University of Michigan. Also, derivatives of this model will be developed for the experimental efforts under FAST, and these will also be modeled and simulated in our new framework so SciML models can be created and validated with the experiments.
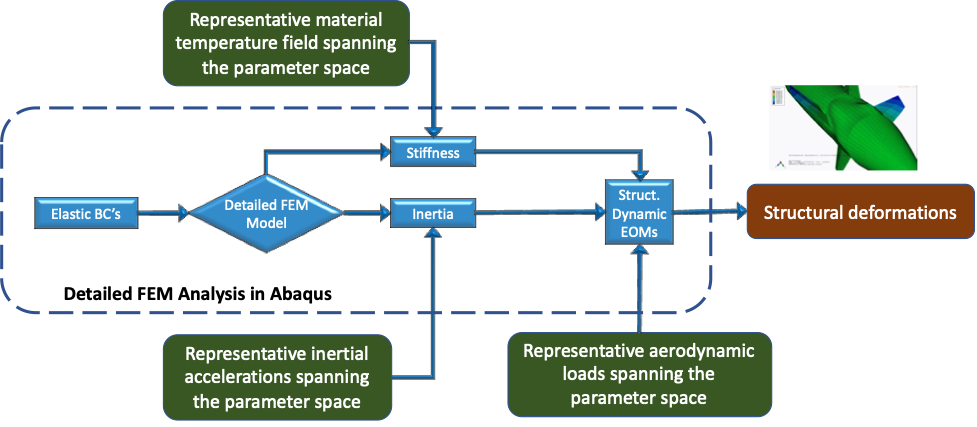
Aerodynamic loadings over the vehicle surface, temperature distribution throughout the structure, and inertial loadings will be used to excite the corresponding structural deformation. Cruise altitude, Mach number, angle of attack, sideslip angle and fin deflections will be varied and sampled using Latin Hypercube Sampling to determine the loading distributions. These approximated loading cases will be fed into the high-fidelity thermoelastic model developed for Abaqus FEM as shown in Figure 2. The corresponding temperature and deformation outputs along with the input loading distributions will then be used to train the machine learning algorithms. Since it is impractical to assume that temperature and elastic deformation are known in many points of the vehicle, we will also investigate the optimal sensor locations to best observe the aerodynamic loads on the vehicle.
Klock, R. J., & Cesnik, C. E. S. (2014). Aerothermoelastic Simulation of Air-Breathing Hypersonic Vehicles. AIAA Science and Technology Forum and Exposition (SciTech2014), National Harbor, Maryland, 13—17 January.
Witeof, Z. D., and Neergaard, L. J. (2014). Initial Concept 3.0 Finite Element Model Definition. In Report AFRL-RWWV-TN-2014-0013 (Issue Eglin Air Force Base: Air Force Research Laboratory).